Пошаговое объяснение:
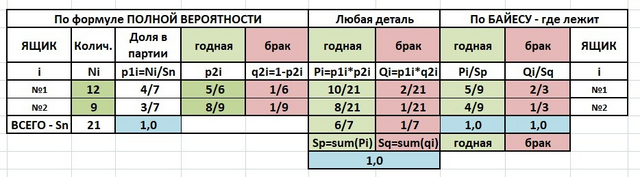
Таблица с расчётами в приложении.
Мысль 1. Смотрим и думаем. В таблице приведен расчет по формулам и полной вероятности и Байеса и, поэтому, есть лишние, но важные для понимания, цифры. Когда решение уже есть, то гораздо легче понять как оно получено.
Мысль 2. Попробуем решить самостоятельно.
Решение.
1) Находим общее число деталей в ящиках - n1=12 и n2=9 и N=21.
2) Находим вероятность Р1 - случайной детали в партии деталей по формуле: p(1,1) = 12/21 = 4/7. p(2.1) = 9/21 = 3/7.
Проверяем на полную вероятность этого события = 1 - правильно.
3) Находим вероятность Р2 -годности детали для каждого ящика по тексту задачи (дано)
р(2,1) = 10/12 = 5/6 и р(2,2) = 8/9 .
ВАЖНО:
1. Описание события по условию задачи: любая деталь из любого ящика будет годной. Два ящика и задача превращается в два события: из первого И годная ИЛИ из второго И годная.
2. Вероятность события "И" - равна произведению вероятностей каждого. Вероятность события "ИЛИ" равна сумме вероятностей каждого.
Продолжаем вычисление вероятности И любой И годной.
Sp= p11 * p21 + p21 * p22 = 10/21+8/21 = 6/7 - ОТВЕТ задачи.
Дополнительно для развития знаний.
Qp = 2/21 + 1/21 = 1/7 = 0,14 (≈ 14%) - любая деталь, но брак.
А теперь по формуле Байеса - какая вероятность, что эта любая деталь из первого ящика.
Всего годных деталей Sp=6/7, и в первом ящике 10/21 годных, а во втором - 8/21. Получаем, что вероятность, что годная деталь из первого ящика = 5/9, а из второго = 4/9 -примерно одинаковая.
А вот вероятность БРАКА в первом ящике в ДВА раза больше, чем во втором (2/3 и 1/3 в таблице).