Ответ: 2 1/3 - площадь.
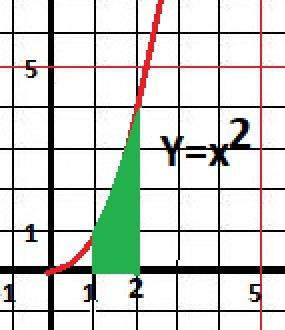
Дано: y₁ = x², y₂ = 0 - две функции.
a = 2, b = 1 - пределы интегрирования.
Найти: S = ? - площадь фигуры.
Думаем: Площадь фигуры равна интегралу разности функций.
Решение:
Записываем интеграл. Подставляем пределы и вычисляем площадь.

Рисунок к задаче в приложении.