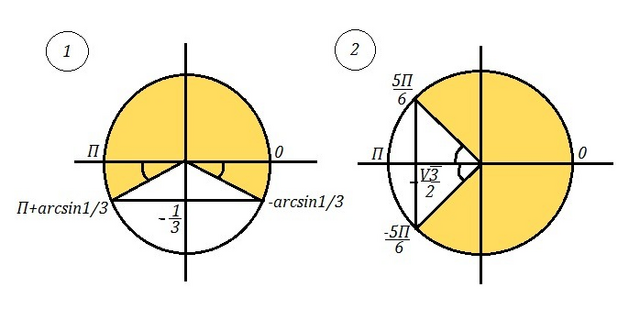
-\frac{1}{3}\\\\-arcsin\frac{1}{3}+2\pi n<\frac{x}{4}<\pi +arcsin\frac{1}{3}+2\pi n\; ,\; n\in Z\\\\-4arcsin\frac{1}{4}+8\pi n<x<4\pi +4arcsin\frac{1}{3}+8\pi n\; ,\; n\in Z" alt="1)\; \; sin\frac{x}{4}\, cos\frac{x}{2}-cos\frac{x}{4}\, sin\frac{x}{2}<\frac{1}{3}\\\\sin(\frac{x}{4}-\frac{x}{2})<\frac{1}{3}\\\\sin(-\frac{x}{4})<\frac{1}{3}\\\\-sin\frac{x}{4}<\frac{1}{3}\\\\sin\frac{x}{4}>-\frac{1}{3}\\\\-arcsin\frac{1}{3}+2\pi n<\frac{x}{4}<\pi +arcsin\frac{1}{3}+2\pi n\; ,\; n\in Z\\\\-4arcsin\frac{1}{4}+8\pi n<x<4\pi +4arcsin\frac{1}{3}+8\pi n\; ,\; n\in Z" align="absmiddle" class="latex-formula">
-\frac{1}{3}\\\\-arcsin\frac{1}{3}+2\pi n<\frac{x}{4}<\pi +arcsin\frac{1}{3}+2\pi n\; ,\; n\in Z\\\\-4arcsin\frac{1}{4}+8\pi n<x<4\pi +4arcsin\frac{1}{3}+8\pi n\; ,\; n\in Z" alt="1)\; \; sin\frac{x}{4}\, cos\frac{x}{2}-cos\frac{x}{4}\, sin\frac{x}{2}<\frac{1}{3}\\\\sin(\frac{x}{4}-\frac{x}{2})<\frac{1}{3}\\\\sin(-\frac{x}{4})<\frac{1}{3}\\\\-sin\frac{x}{4}<\frac{1}{3}\\\\sin\frac{x}{4}>-\frac{1}{3}\\\\-arcsin\frac{1}{3}+2\pi n<\frac{x}{4}<\pi +arcsin\frac{1}{3}+2\pi n\; ,\; n\in Z\\\\-4arcsin\frac{1}{4}+8\pi n<x<4\pi +4arcsin\frac{1}{3}+8\pi n\; ,\; n\in Z" align="absmiddle" class="latex-formula">
 -\frac{\sqrt3}{2}\\\\cos(5x-2x)>-\frac{\sqrt3}{2}\\\\cos3x>-\frac{\sqrt3}{2}\\\\-\frac{5\pi }{6}+2\pi n<3x<\frac{5\pi }{6}+2\pi n\; ,\; n\in Z\\\\-\frac{5\pi }{18}+\frac{2\pi n}{3}<x<\frac{5\pi }{18}+\frac{2\pi n}{3}\; ,\; n\in Z" alt="2)\; \; sin2x\, sin5x+cos2x\, cos5x>-\frac{\sqrt3}{2}\\\\cos(5x-2x)>-\frac{\sqrt3}{2}\\\\cos3x>-\frac{\sqrt3}{2}\\\\-\frac{5\pi }{6}+2\pi n<3x<\frac{5\pi }{6}+2\pi n\; ,\; n\in Z\\\\-\frac{5\pi }{18}+\frac{2\pi n}{3}<x<\frac{5\pi }{18}+\frac{2\pi n}{3}\; ,\; n\in Z" align="absmiddle" class="latex-formula">
-\frac{\sqrt3}{2}\\\\cos(5x-2x)>-\frac{\sqrt3}{2}\\\\cos3x>-\frac{\sqrt3}{2}\\\\-\frac{5\pi }{6}+2\pi n<3x<\frac{5\pi }{6}+2\pi n\; ,\; n\in Z\\\\-\frac{5\pi }{18}+\frac{2\pi n}{3}<x<\frac{5\pi }{18}+\frac{2\pi n}{3}\; ,\; n\in Z" alt="2)\; \; sin2x\, sin5x+cos2x\, cos5x>-\frac{\sqrt3}{2}\\\\cos(5x-2x)>-\frac{\sqrt3}{2}\\\\cos3x>-\frac{\sqrt3}{2}\\\\-\frac{5\pi }{6}+2\pi n<3x<\frac{5\pi }{6}+2\pi n\; ,\; n\in Z\\\\-\frac{5\pi }{18}+\frac{2\pi n}{3}<x<\frac{5\pi }{18}+\frac{2\pi n}{3}\; ,\; n\in Z" align="absmiddle" class="latex-formula">