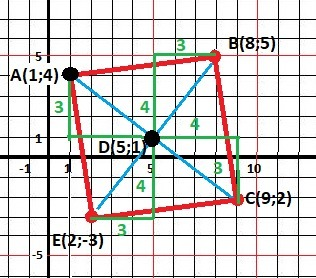
Дано:
А(1;4) - вершина квадрата.
D(5;1) - точка пересечения диагоналей.
Найти: Уравнения сторон квадрата.
Пошаговое объяснение:
Рисунок к задаче в приложении. Решение силой Разума - глазами.
Мысль 1 - диагонали квадрата перпендикулярны, а точка их пересечения делит их по середине.
Мысль 2. Расстояние от т. А до т. D даже не вычисляя (по теореме Пифагора - это будет 3:4:5) - используем катеты - 3 и 4.
Вычисляем координаты вершин используя точку D(5;1) и всего два числа: 3 и 4.
B(8;5), C(9;-2), E(2;-3) - арифметика для первого класса.
2. Уравнения прямых - сторон квадрата - по формуле y = k*x + b находим по координатам двух точек.
ДАНО: A(1;4), B(8;5)
1) k = (Ay-By)/(Ax-Bx)=(4-5)/(1-8)= 1/7 (0,14) - наклон прямой
2) b = Ay-k*Ax=4-(1/7)*1=3 6/7 сдвиг по оси ОУ
Уравнение Y(AB) = x/7+3 6/7 (3,86) - ответ
ДАНО: Е(2;-3), С(9;-2)
1) k = 1/7 - наклон прямой, как и у прямой АВ.
2) b = Еy-k*Еx=-3-(1/7)*2=-3 2/7- сдвиг по оси ОУ
Уравнение Y(ЕС) = x/7- 3 2/7 (3,28) - ответ
ДАНО: Е(2;-3), А(1;4)
1) k = (Еy-Аy)/(Еx-Аx)=(-3-4)/(2-1)=-7 - наклон прямой
2) b = Еy-k*Еx=-3-(-7)*2=11 - сдвиг по оси ОУ
Уравнение Y(ЕА) = -7*x+11 - ответ
ДАНО: В(8;5), С(9;-2)
1) k = -7 - наклон прямой, как и у прямой ЕА.
2) b = Вy-k*Вx=5-(-7)*8=61- сдвиг по оси ОУ
Уравнение Y(ВС) = -7*x+61 - ответ
Задача решена полностью.