ДАНО:Y(x) = (x-5)*(x-2)² = x³ -7*x² + 14*x -20.
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ.
Применим теорему Безу. х1*х2*х*х3 = -20
Один из нулей функции - Х= 5 (действительный, и два мнимых)
3. Интервалы знакопостоянства.
Отрицательная - Х∈(-∞;5], положительная - Х∈[5;+∞).
4. Пересечение с осью OY. Y(0) = -20
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная ни нечётная.
6. Первая производная. Y'(x) = 3*x² -14*x + 14 = 0
.
Корни Y'(x)=0. Х4=1,45 Х5=3,22
Положительная парабола - отрицательная между корнями
7. Локальные экстремумы.
Максимум: Ymax(X4=1,45) =-11,37. Минимум Ymin(X5=3,22) =-14,11
8. Интервалы возрастания и убывания.
Возрастает Х=(-оо;1,45;]U[3,22;+oo) , убывает - Х=[1,45;3,22]
9. Вторая производная - Y"(x) = 6* x -14 = 0
Корень производной - точка перегиба Х₆=2,3
10. Выпуклая “горка» Х∈(-∞; Х₆=2,3]
Вогнутая – «ложка» Х∈[Х₆=2,3) +∞).
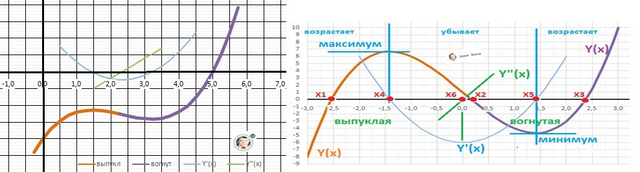
11. График в приложении и рисунок-шаблон для определения интервалов.