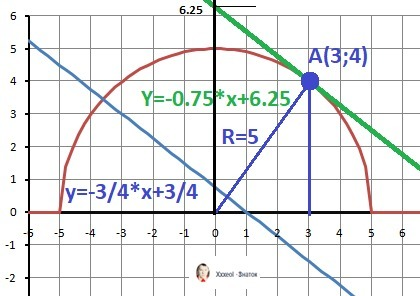
Дано:
Y(x) = √(25-x²) - функция.
3*x + 4*y = 3 - прямая
Пошаговое объяснение:
Рисунок к задаче в приложении.
1. В данном случае это уравнение половины окружности радиусом R=5. (Описан только положительный радикал. Для полной окружности уравнение должно быть по формуле: x²+y²=25).
2. Преобразуем уравнение прямой: y = - 3/4*x + 3/4.
3. Чтобы найти точку касания проводим перпендикулярную линию ОА с коэффициентом наклона k = - 1 /(-3/4) = 4/3.
4. По теореме Пифагора находим точку пересечения: А(3;4).
5. Пишем уравнение касательной параллельной прямой через точку А(3;4).
k= - 3/4 (как и у заданной прямой)
b = Ay - k*Ax = 4 - (-0.75)*3 = 6.25.
y= -0.75*x + 6.25 - уравнение касательной - ответ.