Решить систему уравнений графически X²+y²=36 Y=x²-6

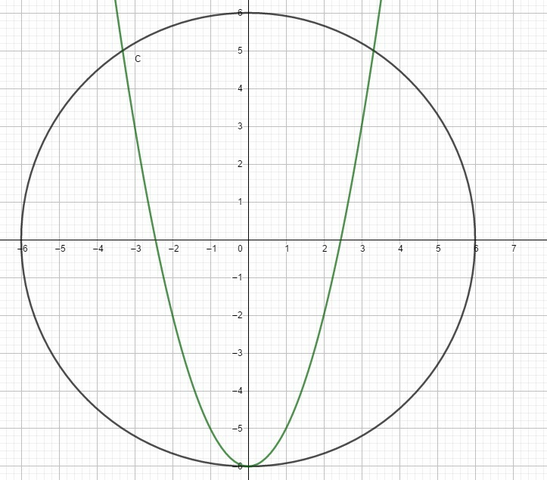
графиком первого уравнения есть окружность с центром (0;0) и радиусом 6 ед.

графиком второго уравнения есть парабола

x=-b/2a=0

y=0-6=-6 с вершиной (0;6)

ответом системы уравнений будет пересечение этих функций

найдем точки пересечения :

$y=-y^2+36-6\\y^2+y-30=0\\y_1=5\\y_2=-6$

точка касания (0;-6)

А точки пересечения :

$5=x^2-6\\x^2-11=0\\x_1=\sqrt{11} \\x_2=-\sqrt{11}$

Ответ: $(-\sqrt{11}; 5),(\sqrt{11};5)$