Вопрос об экстремуме остается открытым:
Тогда возьмем несколько графиков и посмотрим поведение графиков:
 x" alt="y=0;z=-3x^2-24x-2\\z'=-6x-24=0\\x=-4\\-----(+)----(-4)----(-)-->x" align="absmiddle" class="latex-formula">
x" alt="y=0;z=-3x^2-24x-2\\z'=-6x-24=0\\x=-4\\-----(+)----(-4)----(-)-->x" align="absmiddle" class="latex-formula">
х=-4 координата максимума. А что же с у?
 y" alt="x=-4;z=y^3-48+96-2=y^3+46\\z'=3y^2=0\\y=0\\----(+)---(0)---(+)--->y" align="absmiddle" class="latex-formula">
y" alt="x=-4;z=y^3-48+96-2=y^3+46\\z'=3y^2=0\\y=0\\----(+)---(0)---(+)--->y" align="absmiddle" class="latex-formula">
Хм... а вот с игрек координатой вышел косяк. следовательно точка D - точка перегиба, и экстремумов тут нет.
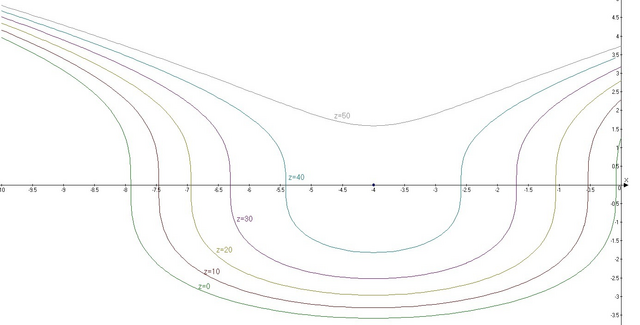
Другой вариант проверки: возьмите любой графический редактор и постройте много-много линий уровня, так чтобы они были близки к исследуемой точке.
Как видно линии уровни не смыкаются к точке экстремума а спокойно пересекают ее.