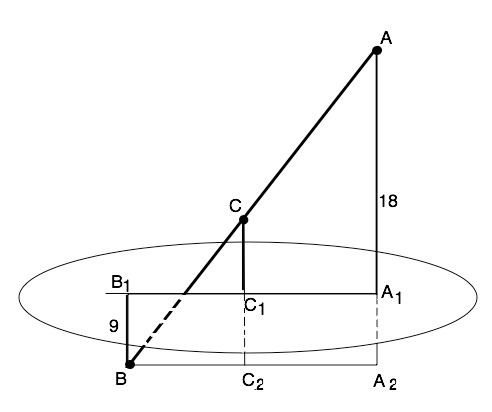
Точки А, В и С принадлежат одной прямой. Прямые АА1, ВВ1 и СС1 параллельны, поэтому лежат в одной плоскости, а точки А1, В1, С1 - на линии пересечения этой плоскости с плоскостью альфа, т.е. на прямой А1В1. Из т.В проведем прямую параллельно В1А1 до пересечения с продолжением АА1 в точке А2. Продолжение СС1 пересечет ВА2 в точке С2. Четырехугольник ВВ1А1А2 -прямоугольник. СС2=А1А2=ВВ1=9 см. Следовательно, в треугольнике АВА2 сторона АА2=18+9=27 см, СС2 как проведенная из середины АВ параллельно АА2 - его средняя линия и равна АА2:2=13,5 см. СС1=СС2-С1С2=13,5-9=4,5 см