Ответ:
6 см
Пошаговое объяснение:
Так как Sabcd = 36 см² = a², a = 6 см (a - сторона квадрата)
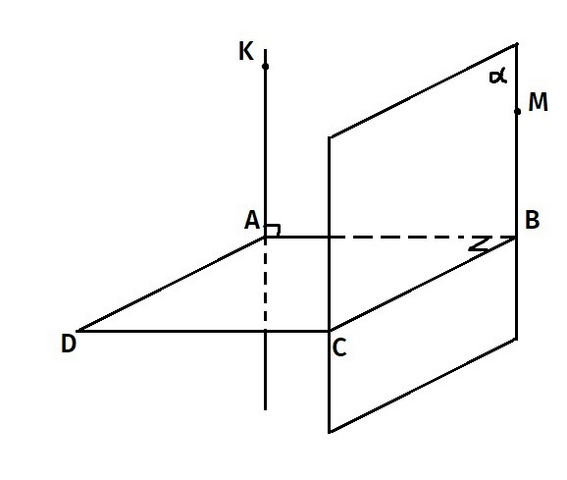
Прямые KA и BC - скрещивающиеся (BC лежит в (ABC), а AK пересекает (ABC) в точке, не лежащей на BC), значит, расстояние между ними - это длина перпендикуляра, опущенного из точки, лежащей на AK, к некоторой плоскости α, содержащей BC и параллельной AK. Такой отрезок - это AB (действительно, AB⊥α, т. к. AB⊥BC; AK||BM, AK⊥(ABC) ⇒ AK⊥AB ⇒ BM⊥AB; BC∩BM). Но AB - это сторона квадрата, а она равна 6 см.