Очень сроооочно!!!!!!

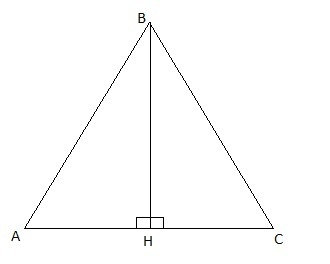
AB = BC = 10 см

BH = 6 см

Из прямоугольного ΔABH:

$AH=\sqrt{AB^2-BH^2}=\sqrt{10^2-6^2}=8$

Т.к. высота равнобедренного треугольника проведенная к основанию одновременно является медианой, то:

AC = 2 * AH = 2 * 8 = 16 см

Площадь треугольника найдем по формуле полупроизведения основания на высоту:

$S=\frac{1}{2}*AC*BH=\frac{1}{2}*16*6=48$

Ответ: площадь треугольника 48 см2