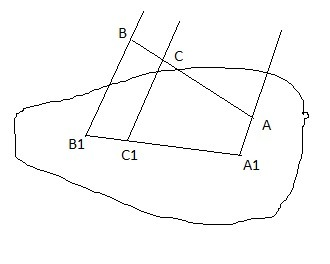
Т.к. через две параллельные прямые можно провести плоскость и притом только одну, то проведем плоскость через прямые AA1 и BB1. Точки A и B принадлежат этой плоскости, а следовательно и прямая AB принадлежит этой плоскости. Точки A1 и B1 принадлежат этой плоскости, а следовательно и прямая A1B1 принадлежит этой плоскости.
Значит задача сводится к планиметрической. Рассмотрим четырехугольник AA1B1B. По условию AA1 ║ BB1, а следовательно это трапеция с большим основанием BB1 и меньшим AA1.
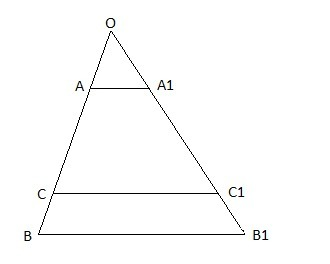
Достроим трапецию до ΔBOB1, продолжив боковые стороны AB и A1B1.
Обозначим BC = x. Тогда CA = 5x.
ΔAOA1 подобен ΔBOB1 по двум углам (∠O общий, ∠OAA1 = ∠OBB1, как соответственный) ⇒

ΔAOA1 подобен ΔCOC1 по двум углам (∠O общий, ∠OAA1 = ∠OCC1, как соответственный) ⇒