Окружности Ω1 и Ω2 равных радиусов пересекаются в точках B и C. ** окружности Ω1 выбрана...

Question

Окружности Ω1 и Ω2 равных радиусов пересекаются в точках B и C. На окружности Ω1 выбрана точка A. Луч AB пересекает окружность Ω2 в точке D (точка B лежит между точками A и D). На луче DC выбрана точка E так, что DC=CE. Найдите AE, если AC=13, AD=10.

Answer 1

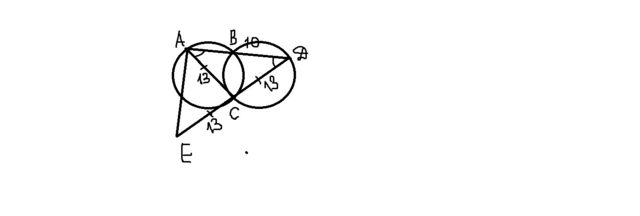
1. Рассмотрим две пересекающиеся окружности. ∠BAC=∠BDC, как вписанные углы, опирающиеся на равные дуги одинаковых окружностей. Исходя из равенства углов, видим, что треугольник ADC - равнобедренный. AC=CD=13.

2. Рассмотрим треугольник AED. По условию, DC=CE, т.е. C - середина стороны ED, а значит отрезок AC - медиана для этого треугольника. Из предыдущего пункта мы знаем, что AC=CD, а значит AC=DC=CE=13.

3. Зная, что AC - медиана, можем написать формулу для ее нахождения:

AC=1/2*√(2*AD²+2*AE²-ED²);

Знаем, что AC=13; AD=10; ED=EC+CD=13+13=26. Получается уравнение, решив которое, найдем AE:

13=1/2*√(2*10²+2*AE²-26²);

13=1/2*√(200+2*AE²-676);

26=√(200+2*AE²-676);

676=200+2*AE²-676;

200+2*AE²=1352;

2*AE²=1152;

AE²=576;

AE=24.

Ответ: AE=24.

---

Comments

Зря загонялся с формулой для вычисления медианы:Здесь медиана равна половине стороны к которой проведена, следовательно это прямоугольный треугольник, а дальше по теореме Пифагора всё проще