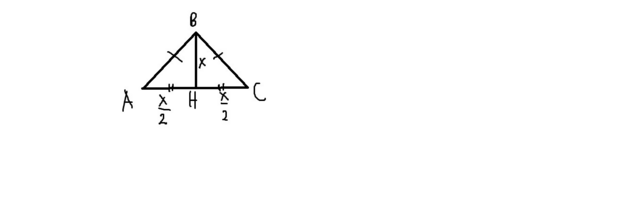1. Пусть имеем равнобедренный треугольник ABC, где AC - основание, AB=BC - боковые стороны. Из вершины B опустим высоту BH на сторону AC. По свойству, высота, опущенная на основание в равнобедренном треугольнике, является и биссектрисой и медианой => AH=HC. Также по условию дано, что BH=AC. Обозначим AC=x, тогда BH=x, AH=HC=x/2.
2. По формуле, связывающей площадь треугольника с радиусом вписанной в него окружности: S=p*r, где S - площадь, p - полупериметр треугольника, r - радиус вписанной окружности.
Площадь треугольника также равна: S=1/2*a*h, где a - основание треугольника, h - высота, опущенная на это основание.
S(ABC)=1/2*AC*BH=1/2*x*x=1/2*x²
3. Рассмотрим прямоугольный треугольник ABH, в котором AH=x/2, BH=x. Тогда, по теореме Пифагора:
AH²+BH²=AB²
x²/4+x²=AB²
AB²=(5*x²)/4
AB=(√5)*x/2
4. Рассмотрим треугольник ABC, в котором AB=BC=(√5)*x/2, AC=x, тогда p (полупериметр) = (AB+BC+AC)/3=((√5)*x+x)/3
5. Подставим все данные в формулу S=p*r (r=2 по условию):
1/2*x²=(((√5)*x+x)/3)*2; | умножим обе части на 2 и раскроем скобки в правой части
x²=(4*(√5)*x+4*x)/3; | разделим обе части на 3
3*x²=4*(√5)*x+4*x; | разделим обе части на x
3*x=4*(√5)+4;
x=(4*(√5)+4)/3.
6. AC=BH=(4*(√5)+4)/3
S(ABC)=1/2*AC*BH=1/2*((4*(√5)+4)/3)²=1/2*((80+32√5+16)/9)=1/2*((96+32√5)/9)=(96+32√5)/18=(48+16√5)/9
Ответ: (48+16√5)/9.