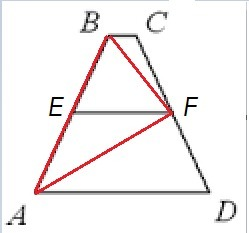
Решение:
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. EF = (BC+AD) /2 = EF = 1 ; BC+AD = 2;
AE=EB. EF - медиана в треугольнике AFB.
Медиана, проведенная из вершины прямого угла, равна половине гипотенузы. AB = 2*EF = 2*1 = 2
Трапеция равнобокая. СD = AB = 2.
Периметр равен p= AB+BC+CD+AD = (AB+CD) +(BC+AD) = (2+2) + 2 = 6
Ответ: p = 6