Дан равнобедренный остроугольный треугольник ABC (AB = BC) , в котором AC = 2. ** боковой...

Question

Дан равнобедренный остроугольный треугольник ABC (AB = BC) , в котором AC = 2. На боковой стороне BC отмечена точка M так, что угол MAC = 40. Точка N лежит на продолжении прямой BC за точку C (C лежит между M и N) так, что AN=MN и угол BAM=NAC . Найти расстояние от точки C до прямой AN .

Answer 1

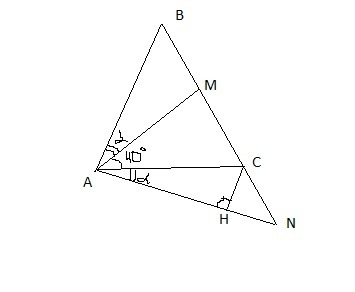
Из точки C опустим высоту CH на отрезок AN, она и будет равна расстоянию от этой точки до прямой.

Обозначим ∠BAM = ∠NAC = α

Тогда ∠BAC = α + 40° ⇒ ∠ACB = α + 40° (т.к. ΔABC равнобедренный)

Из условия равенства суммы углов ΔAMC 180° найдем, что

∠AMC = 180 - 40 - 40 - α = 100 - α

Т.к. ΔAMN равнобедренный (AN = MN), то

∠AMN = ∠MAN ⇒ 100 - α = 40 + α ⇒ α = 30

В прямоугольном ΔACH, против ∠CAH в 30° лежит половина гипотенузы:

CH = AC / 2 = 1

---