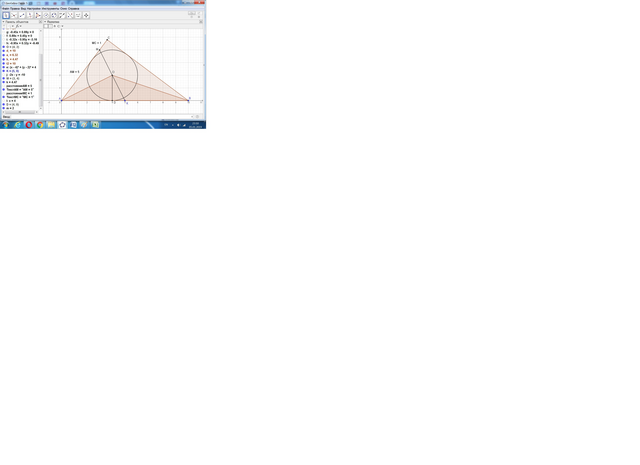
16) Дан треугольник АВС, стороны АС = 6, ВС =8,
Точка О - центр вписанной окружности. Угол АОВ = 135 градусов.
Точка К - середина АВ. Проведена прямая КО, пересекающая АС в точке М.
а) Отрезки АО и ВО - биссектрисы. Сумма углов ОАВ и ОВА равна 180 - 135 = 45 градусов, то есть это сумма половин углов А и В. Полная же сумма углов А и В равна 2*45 = 90 градусов. Поэтому третий угол С равен 180 - 90 = 90 градусов.
б) Гипотенуза АВ = √(6² + 8²) = 10. Проведём ОД ⊥ АВ.
Площадь АВС = (1/2)*6*8 = 24, полупериметр р = (6+8+10)/2 = 12.
Радиус вписанной окружности r = S/p = 24/12 = 2.
Тангенс половинного угла ОАД = sin A/(1 + cos A) = (8/10)/(1 + (6/10)) = 1/2.
Тогда АД = ОД/(1/2) = 2*2 = 4.
Отрезок ДК = (10/2) - 4 = 1.
ОК = √(2² + 1²) = √5.
АО = √(4² + 2²) = √20.
Как видим, в треугольнике АОК сумма квадратов двух сторон равна квадрату третьей: АО² = 20, ОК² = 5, АК² = 25.
Отсюда следует: угол АОК - прямой, биссектриса АО перпендикулярна прямой ОК.
Получаем: АМ = АК = 5.
Ответ: АМ : МС = 5 : 1.