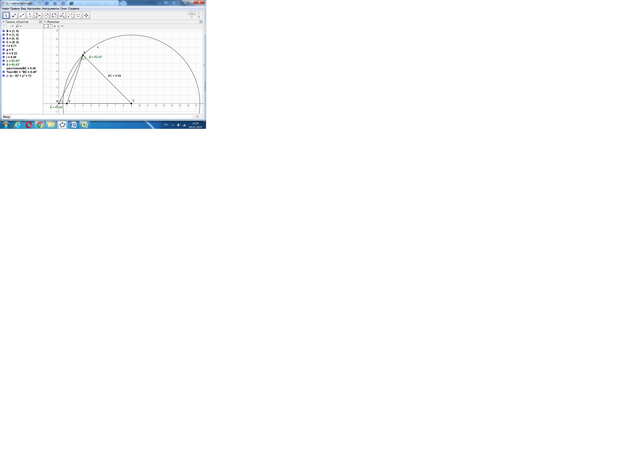
Поместим треугольник АВС точкой А в начало координат, стороной АС по оси Ох. Координаты точек А, Р и С известны: А(0; 0), Р(1; 0), С((9; 0).
Неизвестные координаты точки В примем (х; у).
Из точки В опустим перпендикуляр ВД на АС.
Угол РВС состоит из двух углов: РВД и ДВС.
tg(РВД) = (x - 1)/y, tg(ДВС) = (9 - x)/y.
Находим тангенс суммы углов.
tg(РВД) = (((x - 1)/y) + ((9 - x)/y))/(1 - ((x - 1)/y)*((9 - x)/y)) =
= (x - 1 +9 - x)/(y(у² - (x - 1)*(9 - x)/y).
После приведения подобных и сокращения получаем:
tg(РВД) = 8у/(у² - (x - 1)*(9 - x).
Так как по заданию угол РВД равен углу ВАС тангенс которого равен
у/х, то приравняем: 8у/(у² - (x - 1)*(9 - x) = (у/х).
По свойству пропорции после сокращения на у получаем:
8х = у² - 9х + 9 + х² - х или х² - 18х + 9 + у² = 0.
Выделим полный квадрат по х: (х² - 18х + 81) - 81 +9 + у² = 0.
(х - 9)² + у² = 72.
Получили уравнение окружности с центром в точке С и радиусом R = √72 = 6√2.
То есть, радиусом является искомая сторона ВС.
Ответ: ВС = 6√2 ≈ 8,48528.