Ответ:
Пошаговое объяснение:
sinx≠0, x≠π*n, n∈Z,

Умножим уравнение на  . Получим:
. Получим:



Пусть sinx=y, тогда 
Уравнение имеет корни y=-1 и y=
sinx=-1, x= где n∈Z
где n∈Z
sinx= , x=(-1)ⁿ
, x=(-1)ⁿ , где n∈Z
, где n∈Z
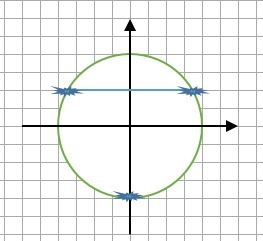
б) отмечая числа на тригонометрическом круге отберем корни принадлежащие промежутку