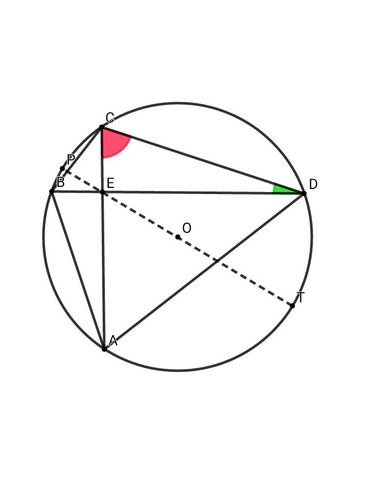
▪ Пусть ∠CDЕ = α , тогда ∠ЕCD = 90° - α
В ΔBCD по т. синусов: ВС/sinα = 2R ⇒ BC = 2R•sinα
В ΔACD по т. синусов: AD/sin( 90° - α ) = 2R ⇒ AD = 2R•cosα
BC² + AD² = ( 2R•sinα )² + ( 2R•cosα )² = 4R²•sin²α + 4R²•cos²α = 4R²•( sin²α + cos²α ) = 4R²
Значит, ( BЕ² + CЕ² ) + ( AЕ² + KЕ² ) = 4R²
▪ По свойству пересекающихся хорд: CE • AE = BE • DE = PE • TE = ( R - d ) • ( R + d ) = R² - d²
AC² + BD² = ( CE + AE )² + ( BE + DE )² = CE² + AE² + BE² + DE² + 2•CE•AE + 2•BE•DE = 4R² + 4( R² - d² ) = 8R² - 4d² = 4•( 2R² - d² )
===================================================================
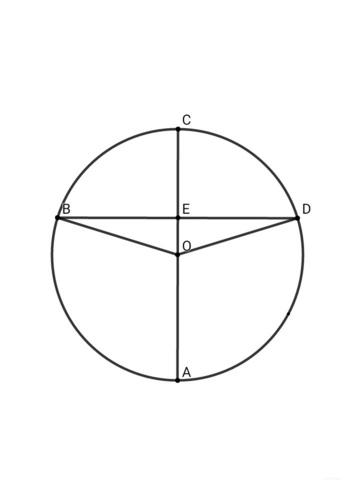
Заметим, что при любом расположении хорд данное значение сохраняется. Пусть АС - диаметр окружности, тогда ОЕ = d
ΔBOD - равнобедренный ( ВО = ОD ) ⇒ OE - высота, биссектриса, медиана ⇒ ВЕ = DE
В ΔOED по т. Пифагора: ЕD = √( OD² - OE² ) = √( R² - d² ) ⇒ BD = 2√( R² - d² )
AC² + BD² = ( 2R )² + ( 2√( R² - d² ) )² = 4R² + 4( R² - d² ) = 8R² - 4d² = 4•( 2R² - d² )
ОТВЕТ: 4•( 2R² - d² )