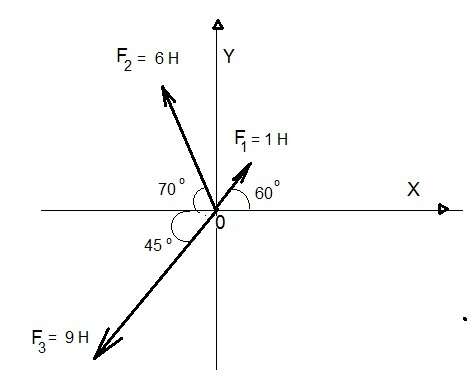
Находим углы:
β1=α1 = 60°
β2=180°-α2 = 180° - 110° = 70°
β3 = α3 - 180° = 225°-180° = 45°
Сделаем чертеж.
Проекция равнодействующей на ось ОХ:
Fx = 1*cos 60° - 6*cos 70° - 9*cos 45° = 1·0,5-6*0,342-9*0,707 ≈ - 7,9 H
Проекция равнодействующей на ось ОY:
Fy = 1*sin 60° - 6*sin 70° - 9*sin 45° = 1*0,866-6*0,940-9*0,707 ≈ - 11,1 H
По теореме Пифагора модуль равнодействующей
F ≈ √ (7,9²+11,1²) ≈ 13,7 Н
Чтобы проверить задачу графически, поступаем следующим образом:
На миллиметровой бумаге с учетом масштаба с помощью линейки и транспортира вычерчиваем векторы сил и углы. Потом по правилу сложения векторов находим равнодействующую.