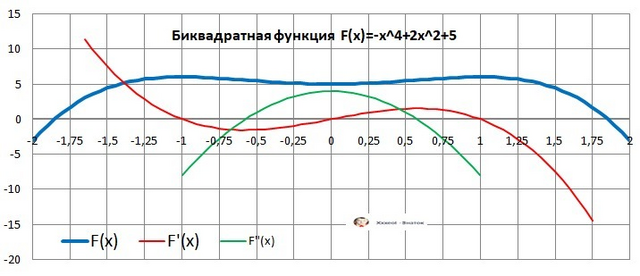
Ответ: E(y) ∈(-∞;6] - область значений функции.
Дано: Y= -x⁴ + 2x²+5.
Пошаговое объяснение:
Для решения задачи надо найти экстремумы функции.
Находим корни первой производной.
Y'(x) = - 4*x³ + 4*x = - 4x*(x² - 1)= - 4*x*(x-1)*(x+1) = 0.
Локальные экстремумы в корнях первой производной.
Ymin(0) = 5 - локальный минимум
Ymax(-1) = Y(1) = 6 - локальный максимум - БОЛЬШЕ НЕ БЫВАЕТ.
ОТВЕТ: E(y)∈(-∞;6].
Рисунок к задаче с графиками - в приложении.