Ответ: 13 - расстояние.
Дано: y = -x² + 10x - 13
Найти: С=? - расстояние от вершины параборлы до О(0;0)
Пошаговое объяснение: Рисунок к задаче в приложении.
Мысль 1. Как найти вершину параболы? Решаем квадратное уравнение и находим корни. Вершина по середине между корнями. Находим координату вершину.
Решаем квадратное уравнение. D = 48, √48 ≈6.928, x1 = 1.536, x2 = 8.464. Середина между корнями - х = 5 и значение У(5) = 12.
Сложно и не точно.
Мысль 2. Привести уравнение к виду: Y = (x+a)² + b.
Преобразуем по формуле "квадрат разности":
y = - (x² - 10x - 13) = - (x²- 2*x*5 + 25) - 13 = - (x-5)²+ 12.
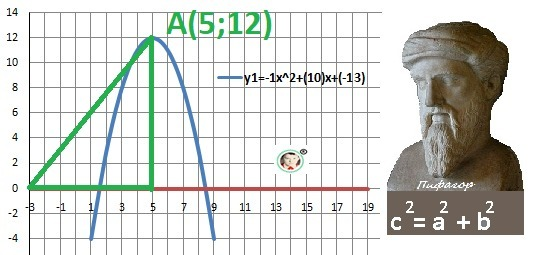
Координаты вершины параболы в точке А(5;12).
И теперь по теореме Пифагора: расстояние между точками О(0;0) и А(5;12)
C² = 5² + 12² = 25 + 144 = 169 = 13²
C=13 - расстояние до вершины - ответ