0\; \; pri\; \; x\in (-\infty ,+\infty )\\\\Otvet:\; x\in [\, \frac{3}{2}\, ,\, +\infty )" alt="1)\; \; |x^2-x+1|\geq |x^2-3x+4|\; \; \to \; \; |x^2-3x+4|\leq |x^2-x+1|\\\\\star \; \; |A|0\; \; pri\; \; x\in (-\infty ,+\infty )\\\\Otvet:\; x\in [\, \frac{3}{2}\, ,\, +\infty )" align="absmiddle" class="latex-formula">
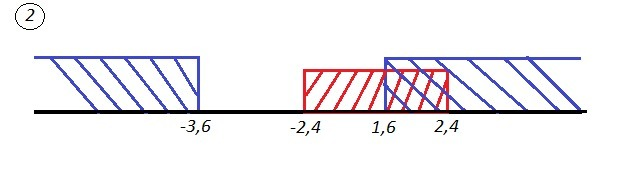
-x}} \right. \; \left \{ {{x^2-6<0} \atop {x^2+2x-6>0}} \right. \\\\a)\; \; x^2-6<0\; ,\; \; (x-\sqrt6)(x+\sqrt6)<0\; ,\; \sqrt6\approx 2,4\\\\znaki:\; \; +++(-\sqrt6)---(\sqrt6)+++\quad x\in (-\sqrt6,+\sqrt6)\\\\b)\; \; x^2+2x-6>0\; ,\; \; D/4=1+6=7\; ,\; x_{1,2}=-1\pm \sqrt7\\\\(x+1-\sqrt7)(x+1+\sqrt7)>0\\\\znaki:\; \; \; +++(-1-\sqrt7)---(-1+\sqrt7)+++\\\\x\in (-\infty ,-1-\sqrt7)\cup (-1+\sqrt7,+\infty )" alt="2)\; \; |x^2+x-6|-x}} \right. \; \left \{ {{x^2-6<0} \atop {x^2+2x-6>0}} \right. \\\\a)\; \; x^2-6<0\; ,\; \; (x-\sqrt6)(x+\sqrt6)<0\; ,\; \sqrt6\approx 2,4\\\\znaki:\; \; +++(-\sqrt6)---(\sqrt6)+++\quad x\in (-\sqrt6,+\sqrt6)\\\\b)\; \; x^2+2x-6>0\; ,\; \; D/4=1+6=7\; ,\; x_{1,2}=-1\pm \sqrt7\\\\(x+1-\sqrt7)(x+1+\sqrt7)>0\\\\znaki:\; \; \; +++(-1-\sqrt7)---(-1+\sqrt7)+++\\\\x\in (-\infty ,-1-\sqrt7)\cup (-1+\sqrt7,+\infty )" align="absmiddle" class="latex-formula">
