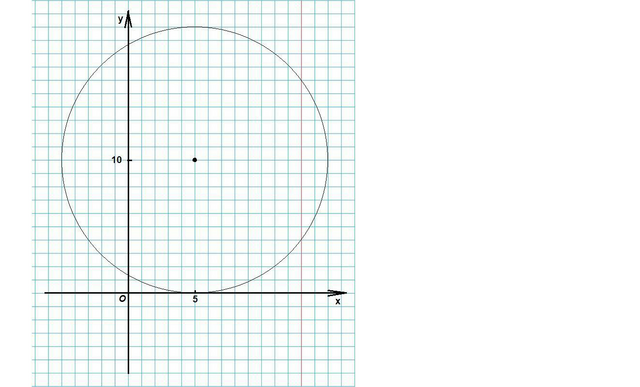
Ответ:
b) прямая является касательной к окружности.
Объяснение:
Уравнение окружности имеет вид
(x - x₀)² + (y - y₀)² = R², где
(x₀; y₀) - координаты центра окружности,
R - радиус окружности.
(x - 5)² + (y - 10)² = 100
(5; 10) - центр окружности,
R = √100 = 10 - радиус окружности.
а) Окружность изображена на рисунке.
b) Расстояние от центра окружности до прямой у = 20:
d = |y₀ - 20| = |10 - 20| = |- 10| = 10
d = R = 10
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности.