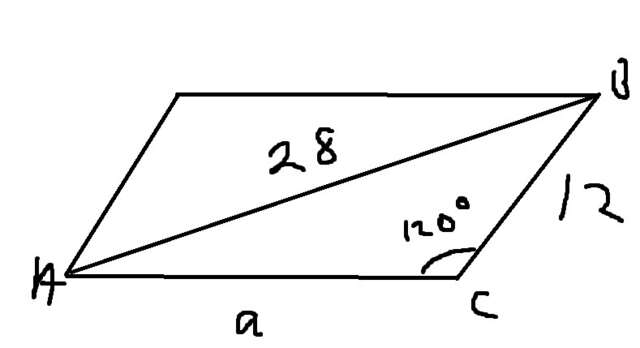
Применим теорему косинусов для треугольника ABC;
28² = 12²+a²-2×12×a×cos120°
28² = 144+a²+12a;
a² +12a +144 - 784 = 0;
a²+12a - 640 = 0;
Решаем квадратное уравнение, корни которого:
a1 = -32; ( не удовлетворяет условию ) т,к сторона не может быть отрицательной.
a2 = 20;
Значит вторая сторона параллелограмма - 20 см.
P = 2(a+b) , где a,b - стороны параллелограмма.
P = 2*32 = 64 см