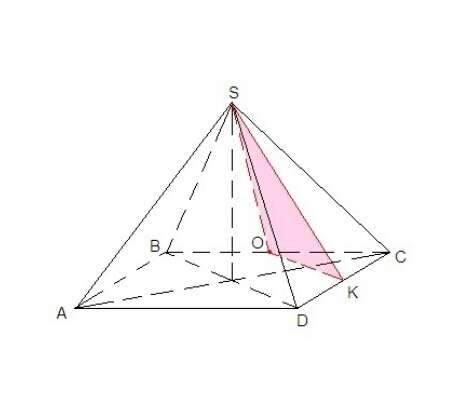
Отметим точку К - середину ребра CD.
Искомое сечение SOK, так как оно проходит через прямую SO и прямую ОК, параллельную прямой BD (ОК║BD как средняя линия треугольника BCD). А если прямая BD параллельна прямой, лежащей в сечении, то она параллельна секущей плоскости.
Пирамида правильная, значит в основании квадрат. Все ребра по 6 см, значит боковые грани - равные равносторонние треугольники.
Диагональ квадрата равна а√2, где а - сторона квадрата.
BD = 6√2 см
ОК = BD/2 = 3√2 см
SO = SK как высоты равных равносторонних треугольников,
SO = SK = a√3/2 = 6√3/2 = 3√3 см (а - ребро пирамиды)
Psok = SO + SK + OK = 3√3 + 3√3 + 3√2 = 6√3 + 3√2 = 3(2√3 + √2) см