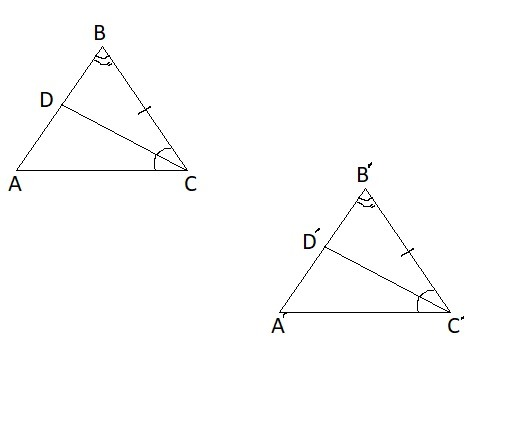
По условию BC = B'C' и CD = C'D'
Т.к. ∠ACB = ∠A'C'B', то равны и их половины: ∠DCB = ∠D'C'B'
Следовательно ΔBCD = ΔB'C'D' (по двум сторонам и углу между ними).
Из равенства этих треугольников следует, что ∠DBC = ∠D'B'C'
Тогда ΔABC = ΔA'B'C' (по стороне и двум прилегающим углам).
Т.е. AC = A'C'