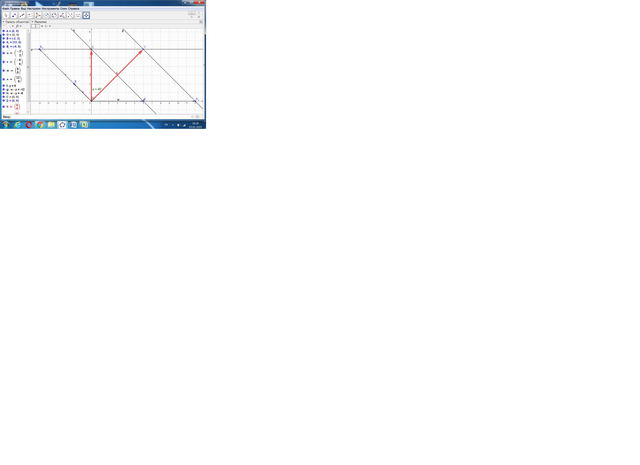
2,04) Находим модули векторов 2a и 3b:
2а = 6*2 = 12,
3b = 3*(2√2) = 6√2.
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
Fрез. = √(F1² + F2² -2 F1 F2 cos(180°-α)).
c = 2a + 3b = √(12² + (6√2)² - 2*12*6√2*(√2/2)) = √(144 + 72 - 144) = 6√2.
d = a + 3b = √(6² + (6√2)² - 2*6*6√2*(√2/2)) = √(36 + 72 - 72) = 6.
где F = числовое значение вектора
α = угол между векторами 1 и 2 (α = 3π/4 = 135°, 180 - α = 45°).
Получили 2 вектора длиной 6√2 и 6.
Расстояние между их концами равно 2а - а = а = 6.
Это получился равнобедренный прямоугольный треугольник.
Ответ: угол (c∧d) = 45°.
Это угол можно получить как разницу углов между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
β = arcsin( F2 *sin(180°-α) / Fрез.)
где α = угол между исходными векторами