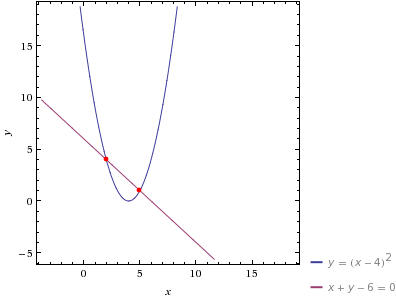
площадь фигуры №3
y=x^2-8x+16
x+y-6=0 ; y=6-x
приравняем правые части , найдем общие корни
x^2-8x+16=6-х
x^2-7x+10=0
D=9
x1=5 x2=2
координаты точек пересечения
(2;4) (5;1)
S =S1 -S2
S искомая площадь
S1 площадь трапеции/фигура над параболой
S2 площадь фигуры под параболой/кривой
S1=1/2*(y2+y1)*(x2-x1)=1/2*(4+1)*(5-2)=1/2 *5*3=15/2
S2=[2-5] ∫( x^2-8x+16)= x^3 /3-4x^2+16x │[2-5]= (5^3 /3-4*5^2+16*5) -( 2^3 /3-4*2^2+16*2) =3
S =S1 -S2 = 15/2- 3 = (15-6)/2=9/2=4,5
ответ 4,5