Ответ:
Пошаговое объяснение:
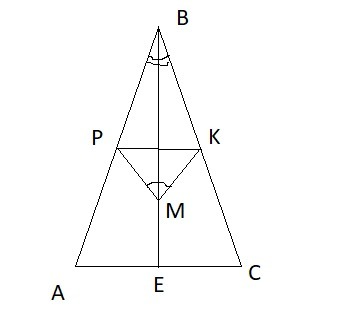
а) Медиана проведенная к основанию равнобедренного треугольника является одновременно его биссектрисой, следовательно ∠PBM = ∠KBM. По условию ∠BMP = ∠BMK.
Следовательно ΔBPM = ΔBKM (у них общая сторона BM. к которой прилегают два равных угла). Из равенства этих треугольников и следует, что ∠BPM= ∠BKM.
б) В пункте а) доказано, что ΔBPM = ΔBKM, откуда следует, что BP = BK. Следовательно PK || AC.
А AC ⊥ BE (т.к. медиана проведенная к основанию равнобедренного треугольника является одновременно его высотой). Значит и PK ⊥ BE ⇒ PK ⊥ BM