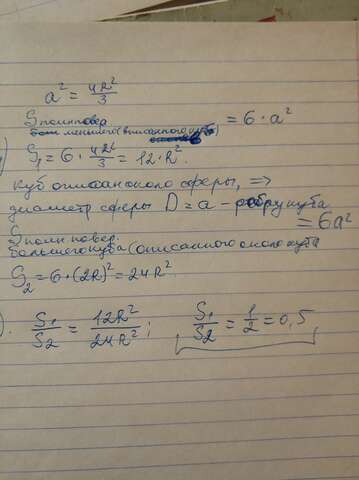По условию известно, что в сферу вписан куб, следовательно, диаметр сферы D = диагонали куба d
теорема о квадрате диагонали прямоугольного параллелепипеда:
d^2 = a^2+b^2+c^2
куб - прямоугольный параллелепипед, все ребра, которого равны а
d^2=3a^2
D=2R
d=2R
(2R)^2=3a^2
4R^2=3a^2
продолжение во вложении