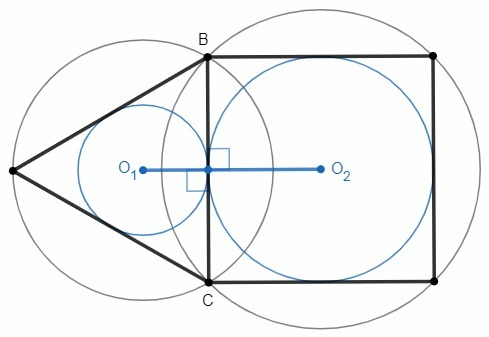
В правильном многоугольнике центры вписанной и описанной окружности совпадают.
Расстояние до стороны BC - радиус вписанной окружности в обеих фигурах.
Радиус вписанной окружности равностороннего треугольника a√3/6
Радиус вписанной окружности квадрата a/2
O1O2 =a√3/6 +a/2 =1+√3