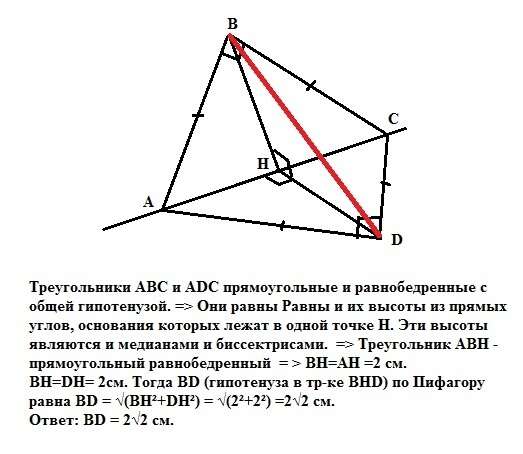
Треугольники АВС и ADC прямоугольные и равнобедренные с общей гипотенузой. => Они равны. Равны и их высоты из прямых углов, основания которых лежат в одной точке Н. Эти высоты являются и медианами и биссектрисами. => Треугольник АВН - прямоугольный равнобедренный = > ВН=AH =2 см.
ВН=DH= 2см. Тогда BD (гипотенуза в тр-ке ВНD) по Пифагору равна
BD = √(BH²+DH²) = √(2²+2²) =2√2 см.
Ответ: ВD = 2√2 см.