ДАНО:
y = -2*x³ + 6*x² + 5.
D(y) =[-2;2]
Найти: Экстремумы.
Пошаговое объяснение:
Находим точки экстремума по первой производной.
Y'(x) = -6*x² + 12*x = -6*x*(x-2) = 0.
Корни - точки экстремумов - Х1 = 0 и Х2 = 2.
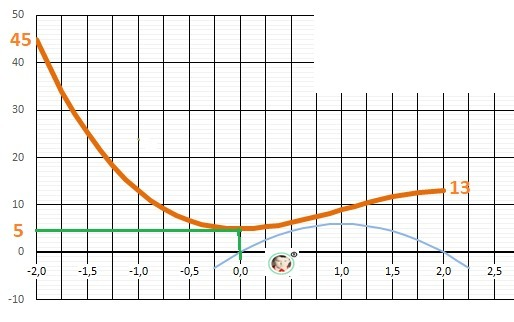
Локальный минимум- Y(0) = 5, локальный максимум - Y(2)=13.
Но на границе D(y) = - 2 - значение Y(-2) = 45.
Рисунок с графиком функции в приложении.
Ответ: Ymax(-2) = 45, Ymin(0) = 5.