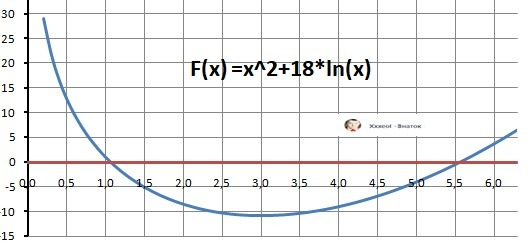
Дано: f(x) = x² - 18*㏑x
Пошаговое объяснение:
1) Область определения. X>0. D(y) -X∈(0;+∞).
2) Первая производная.

3) Корни производной: х = 3. Значение х = -3 - не входит в D(y).
4) Локальный экстремум: минимум - f(3) = - 10.775 - ответ.
5) Интервалы монотонности.
Убывает - X∈(0;3], возрастает - X∈[3;+∞) - ответ
6) График функции в приложении - подарок.