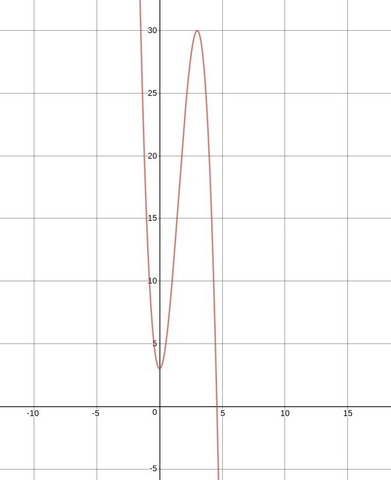
Ответ:
Точка (3; 30)
Пошаговое объяснение:

Для нахождения экстремумов найдём производную:

В экстремумах функции производная обращается в ноль.Следовательно, экстремумы функции - точки  и
и  .
.
Найдём вторую производную, чтобы понять чем является экстремум - локальным минимумом или локальным максимумом:
 0 \Rightarrow x_1 - \min\\y''(x_2) = -18 < 0 \Rightarrow x_2 - \max" alt="y'' = -12x + 18\\y''(x_1) = 18 > 0 \Rightarrow x_1 - \min\\y''(x_2) = -18 < 0 \Rightarrow x_2 - \max" align="absmiddle" class="latex-formula">
0 \Rightarrow x_1 - \min\\y''(x_2) = -18 < 0 \Rightarrow x_2 - \max" alt="y'' = -12x + 18\\y''(x_1) = 18 > 0 \Rightarrow x_1 - \min\\y''(x_2) = -18 < 0 \Rightarrow x_2 - \max" align="absmiddle" class="latex-formula">
Найдём значение в локальном максимуме:
 .
.
В качестве приложения - график: