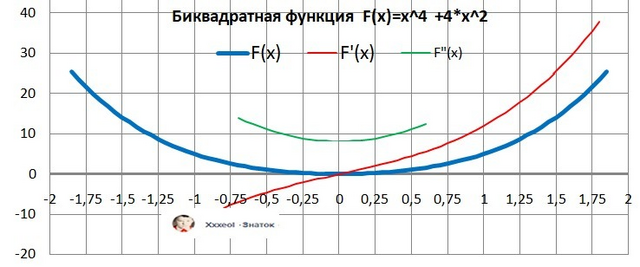
Дано: y = x⁴ + 4*x²
Исследование:
1. Область определения: D(y)= R, X∈(-∞;+∞)
Непрерывная. Разрывов нет. Вертикальных асимптот - нет
2. Нули функции: y = х²*(х²+4) = 0. Х=0.
3. Пересечение с осью ОУ - Y(0) = 0
4. Интервалы знакопостоянства.
Y(x) >0 - X∈(-∞;+∞)
5. Четная: Y(-x) = Y(x)
6. Первая производная.
Y'(x) = 4*x³ + 8*x = x*(x² + 8) = 0
Точка экстремума: x = 0
7. Локальный экстремум: Ymin(0) = 0
8. Интервалы монотонности.
Убывает - X∈(-∞;0], возрастает - X∈[0;+∞)
9. Вторая производная
Y"(x) = 12*x² + 8 = 0 - точки перегиба - нет. Y"(x)>0
10. Вогнутая - "ложка" - X∈(-∞;+∞)
11. График функции в приложении.