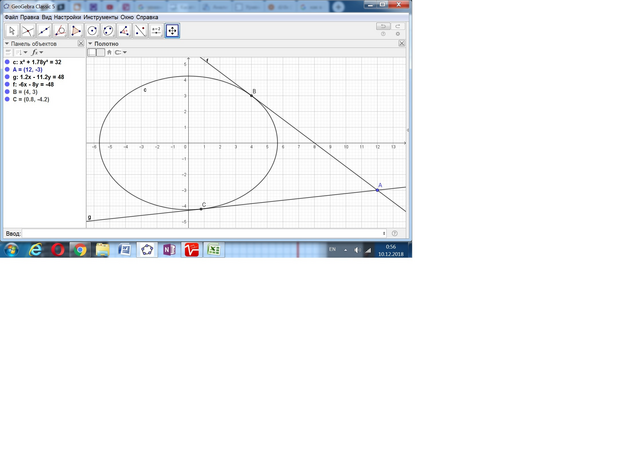
Дан эллипс (х²/32) + y²/18) = 1 и точка А(12; -3).
Выразим функцию относительно у.
у = +-√(288 - 9х²)/4 = +-(3/4)√(32 - х²).
уравнение касательной эллипса, проходящей через эту точку:
(xx0/a²) + (yy0/b²) = 1.
Подставим координаты точки А(12; -3).
(12x0/32) + (-3y0/18) = 1.
Значение у0 заменим из функции: у0 = +-(3/4)√(32 - х0²).
Приведя к общему знаменателю и сократив на 2, получаем квадратное уравнение 5х0² - 24х0 + 16 = 0.
Ищем дискриминант:
D=(-24)^2-4*5*16=576-4*5*16=576-20*16=576-320=256;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√256-(-24))/(2*5)=(16-(-24))/(2*5)=(16+24)/(2*5)=40/(2*5)=40/10=4;
x_2=(-√256-(-24))/(2*5)=(-16-(-24))/(2*5)=(-16+24)/(2*5)=8/(2*5)=8/10=0.8.
Подставив значения х в уравнение, находим координаты точек касания по у: у_1 = 3, у_2 = 21/5 = 4,2.
С учётом того, что вторая точка касания находится в отрицательной полуплоскости, значение у_2 = -4,2.
Подставив координаты точек в уравнение касательной. получаем 2 уравнения:
у = (-3/4)х + 6,
у = (3/28)х - (30/7).