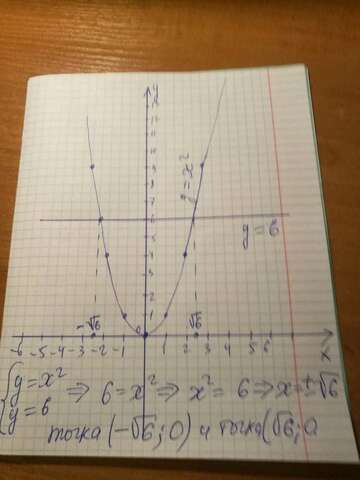
Ответ: ПОСТРОИМ ГРАФИК ПАРАБОЛЫ У = Х² И ПРЯМОЙ У=6 В ОДНОЙ ПЛОСКОСТИ.
ЧТОБЫ ОПРЕДЕЛИТЬ ТОЧКИ ПЕРЕСЕЧЕНИЯ ГРАФИКОВ ФУНКЦИЙ РЕШИМ СИСТЕМУ УРАВНЕНИЙ У = Х ² и У = 6 , ОТКУДА Х² = 6 И имеем два корня Х = √6 и Х = - √6
получаем две точки пересечения графиков данных функций (- √6; 6) и ( √6; 6)
абсциссы точек пересечения это значения по оси ОХ: - √6 и +√6
√4 <√6< √9 поэтому 2 < √6 < 3 и в отрицательной части оси ОХ - 3 < - √6 < - 2 </strong>
Пошаговое объяснение: