Мистер Фокс нарисовал квадрат со стороной 1. Затем он разделил обе его горизонтальные...

Question

47 просмотров

Мистер Фокс нарисовал квадрат со стороной 1. Затем он разделил обе его горизонтальные стороны на 120 равных частей и провел 119 вертикальных отрезков, соединяющих соответствующие точки. После этого он разбил обе вертикальные стороны на 90 равных частей и провел горизонтальные отрезки, соединяющие соответствующие точки. Сколько разных (то есть имеющих разные стороны) квадратов можно увидеть на получившемся рисунке? Разные квадраты - это квадраты разного размера.

Математика Natagasyuk_zn (37 баллов) 24 Май, 20 | 47 просмотров

Дан 1 ответ

Правильный ответ

Ответ:

30 видов квадратов

Пошаговое объяснение:

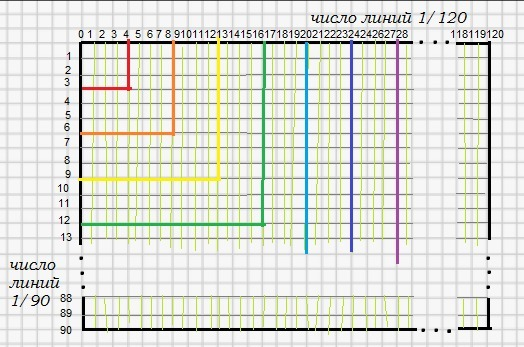
Равные стороны квадрата со стороной 1 разделены на разные по величине отрезки. Горизонтальная сторона на 120 частей, а вертикальная - на 90.

1/90 : 1/120 = 1/3 : 1/4 = 4 : 3 ----- отношение величин отрезков

Т.е. 3 части по 1/90 вертикальной стороны соответствуют по величине 4 частям по 1/120.

3/90 = 4/120

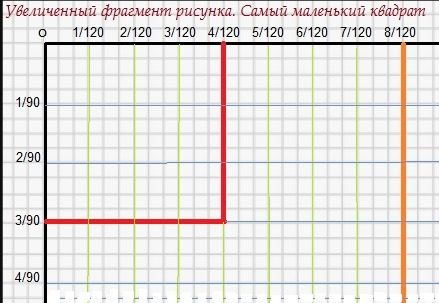
3/90 Х 4/120 ---- это самый маленький квадрат

Если добавлять каждый раз с вертикальной стороны по 3 отрезка(3*1/90=3/90), а с горизонтальной стороны по 4 отрезка (4*1/120=4/120), получим последовательность увеличивающихся в размере квадратов, самый большой из которых - исходный, со стороной 90/90 (или 120/120)

3/90; 6/90; 9/90; ... ; 84/90; 87/90; 90/90

Формула общего члена этой последовательности:

$\displaystyle a_{n}=a_{1} +(n-1)*d$

Отсюда мы можем найти число разных квадратов n:

$\displaystyle n = \frac{(a_{n}- a_{1}) }{d}+1$

аn = 90/90; а₁ = 3/90; d = а₂ - а₁ = 6/90 - 3/90 = 3/90

n = (90/90 - 3/90)/(3/90) + 1

n = 30

Ответ: 30 видов квадратов ( с разными сторонами)

helenaal_zn (114k баллов) 24 Май, 20