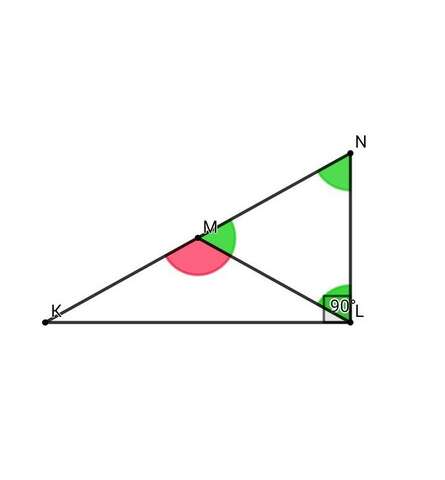
9) Рисунок 1: тр. KML - равнобедренный ( КМ = МL )
▪ Отложим отрезок МN, равный отрезку KM, на её продолжении ***** угол NML = 180° - 120° = 60° ***** тр. NML - равносторонний, то есть на стороне ML построили равносторонний треугольник внешним образом ***** KM = ML = MN = NL = x
▪ По теореме Пифагора в тр. KNL:
KN^2 = KL^2 + NL^2

☆ ОТВЕТ: х = 12V3 ☆
10) тр. RTS - прямоугольный , угол Т = 90°
▪ По теореме Пифагора в тр. RTS:
RS^2 = RT^2 + TS^2
TS^2 = 13^2 - 12^2
TS^2 = 169 - 144 = 25
TS = 5
▪ Площадь треугольника RTS:
S rts = TM • RS / 2 = RT • TS / 2
TM • RS = RT • TS
TM = RT • TS / RS = 12 • 5 / 13 = 60 / 13 = 4_8/13
☆ ОТВЕТ: х = 4_8/13 ☆
11) ▪тр. АСВ - равнобедренный ( АС = СВ )
CD - высота, медиана, биссектриса **** AD = DB = 10/2 = 5
▪ По теореме Пифагора в тр. BCD:
CD^2 = 13^2 - 5^2 = 169 - 25 = 144
CD = 12
▪Плошадь тр. АСВ:
S acb = CD • AB / 2 = AE • CB / 2
CD • AB = AE • CB
AE = CD • AB / CB = 12 • 10 / 13 = 120 / 13 =
9_3/13
☆ ОТВЕТ: х = 9_3/13 ☆
12) KMRN - ромб ( KM = MR = RN = KN )
▪Диагонали ромба взаимно перпендикулярны, делящие ромб на 4 равных прямоугольных треугольника. Диагонали ромба точкой пересечения делятся пополам ***** Пусть точка О - точка пересечения диагоналей ромба ***** KO = OR = 10/2 = 5 ***** MO = ON = 12/2 = 6
▪ По теореме Пифагора в тр. МОК:
МК^2 = 5^2 + 6^2 = 25 + 36 = 61
МК = V61
☆ ОТВЕТ: х = V61 ☆
13) АBCD - ромб ( AB = BC = CD = AD )
▪Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам ***** Пусть точка О - точка пересечения диагоналей ромба ***** ВO = OD = 12/2 = 6
▪По теореме Пифагора в тр. ВОС:
ОС^2 = 10^2 - 6^2 = 100 - 36 = 64
ОС = 8
АС = 2•ОС = 2•8 = 16
☆ ОТВЕТ: х = 16 ☆
14)
▪Применим для тр. MNK теорему Пифагора:
MK^2 = MN^2 + NK^2
25^2 = 7^2 + 24^2
625 = 49 + 576
625 = 625
Следовательно, по теореме, обратной теореме Пифагора, следует, что тр. МNK - прямоугольный ( угол N = 90° )
▪ Площадь тр. MNK:
S mnk = NL • MK / 2 = MN • NK / 2
NL • MK = MN • NK
NL = MN • NK / MK = 7 • 24 / 25 = 168/25 = 6,72
☆ ОТВЕТ: х = 6,72 ☆
15) SRLK - прямоугольник
▪Очевидно, что в этой задаче не хватает данных для её решения
Допустим, что в условии задачи известна сторона KS = 5, тогда
▪ По теореме Пифагора в тр. LKS:
SL^2 = KS^2 + KL^2
SL^2 = 5^2 + 12^2 = 25 + 144 = 169
SL = 13
☆ ОТВЕТ: х = 13 ☆
16)
▪ Применим для тр. МКТ теорему Пифагора:
МТ^2 = КТ^2 + МК^2
34^2 = 30^2 + 16^2
1156 = 900 + 256
1156 = 1156
Значит, по теореме, обратной теореме Пифагора, следует, что тр. МКТ - прямоугольный ( угол К = 90° )
▪Пропорциональные отрезки в прямоугольном треугольнике:
МК^2 = MN • MT
16^2 = MN • 34
256 = MN • 34
MN = 256/34 = 128/17 = 7_9/17
☆ ОТВЕТ: х = 7_9/17 ☆