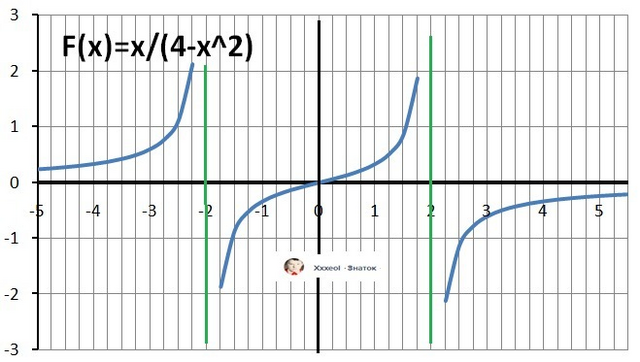
Ответ:
Пошаговое объяснение:
1) Область определения (4-х²)≠0, x≠-2, x≠+2
D(y) - X∈ (-∞;-2)∪(-2;2)∪(2;+∞)
2) Локальные экстремумы в корнях первой производной.

Вещественных корней нет.
Рисунок с графиком функции в приложении.
Возрастает везде, где существует.
ОТВЕТ X∈ (-∞;-2)∪(-2;2)∪(2;+∞)