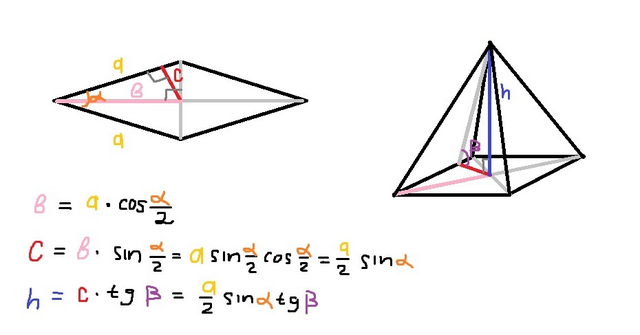Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам.
1) Две полудиагонали и сторона ромба образуют прямоугольный треугольник с одним из острых углов = alpha / 2; сторона ромба является гипотенузой, а одна из полудиагоналей (b) является катетом, прилежащим к этому углу -> длина этой полудиагонали = a * cos(alpha / 2)
2) Опущенная в этом треугольнике на гипотенузу (сторону ромба) высота (c) образует еще один прямоугольный треугольник с полудиагональю (b) и соответствующей частью стороны ромба; гипотенуза этого треугольника - полудиагональ (b) ромба, высота является катетом, лежащим напротив угла alpha / 2 - ее длина = длина полудиагонали * sin(alpha/2) = a * sin(alpha/2) * cos(alpha/2) = a/2 * sin(alpha)
3) Высота треугольника (c) и высота пирамиды (h) образуют прямоугольный треугольник, угол напротив высоты пирамиды = beta -> высота пирамиды (h) = высота треугольника (с) * tg( beta ) = a/2 sin(alpha) tg(beta)