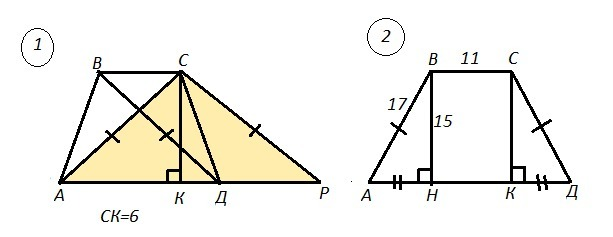
1) АВСД - трапеция , АВ=СД ⇒ АС=ВД , СК⊥АД , СК=6 см.
Средняя линия трапеции m=12 cм, высота СК=6 см .
m=(АД+ВС)/2 ⇒ 2m=АД+ВС , АД+ВС=12·2=24 (см).
ВД и АС - диагонали, ВД=АС .
Проведём СР║ВД ⇒ ВСРД - параллелограмм ⇒ СР=ВД , ДР=ВС.
АС=СР ⇒ ΔАСР - равнобедренный. СК⊥АР ⇒ СК - высота и медиана в равнобедренном треугольнике ⇒ АК=КР .
АР=АД+ДР=АД+ВС=m=24 см , АК=КР=АР:2=12 см.
ΔАКС: ∠АКС=90° ,
диагональ АС=√(АК²+СК²)=√(12²+6²)=√180=6√5 (см).
2) АВСД - трапеция , АВ=СД=17 см, ВС=11 см, ВН⊥АД , ВН=15 см.
Проведём СК⊥АД , ВСКН - прямоугольник ⇒
ВС=НК=11 см, ВН=СК=15 см ⇒ ΔАВН=ΔСДК ⇒ АН=КД .
Из ΔАВН: АН=√(АВ²-ВН²)=√(17²-15²)=8
АД=АН+НК+КД=8+11+8=27 (см)