Найти направление выпуклости и точки перегибая кривой. построение кривых y=х4/х³-1

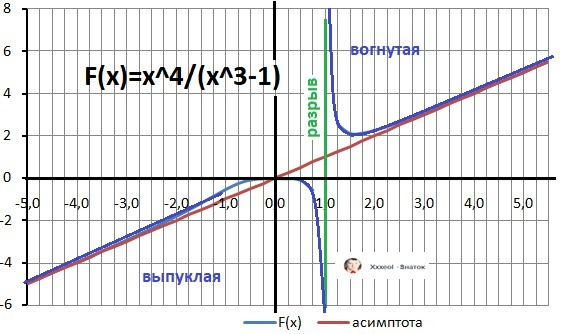
Пошаговое объяснение:

1. Область определения - х≠ 1. Разрыв при х=1.

2. Вычисляем поведение функции вблизи точки разрыва.

limY(-1-)(x) = - ∞ - график идёт вниз и limY(-∞)(x) = - ∞ - график идёт вниз. Выпуклая при Х∈(-∞;1)

limY(-1+)(x) = + ∞ - график идёт вверх, limY(+∞)(x) = + ∞ - график идёт вверх. Вогнутая при Х∈(1;+∞)

Находим наклонную асимптоту функции - делим и числитель и знаменатель на х³ (степень в знаменателе)..

Y = lim(+∞)Y(x)/x³ = (Х+0)/(1+0) = Х

Вывод: точка Х = 1 - точка перегиба -

График функции на рисунке в приложении.

Это решение силой Разума. А теперь - высшая математика.

Направление выпуклости определяем по знаку второй производной.

Если положительна - вогнутая (как у Y=x², Y"(x)=2)

$Y'(x)=\frac{4x^3}{x^3-1}-\frac{3x^6}{(x^3-1)^2}$ - первая производная

$Y"(x)=\frac{12x^2}{x^3-1}-\frac{24x^5}{(x^3-1)^2}+\frac{18x^4}{(x^3-1)^3}-\frac{6x}{(x^3-1)^4}$

- вторая производная функции.