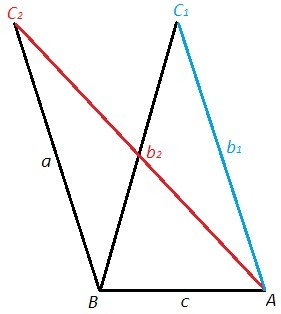
a=7, c=4, S=6√5
Площадь треугольника через две стороны и угол между ними:
S= ac*sinB /2 <=> sinB= 2S/ac =3√5/7
cosB= √(1-(sinB)^2) =√(1 -45/49) =√(4/49) = +-2/7
Теорема косинусов:
b= √(a^2 +c^2 -2ac*cosB)
b1= √(49 +16 -16) =√49 =7
b2= √(49 +16 +16) =√81 =9
Радиус вневписанной окружности (к стороне b):
p=(a+b+c)/2 (полупериметр)
r_b= S/(p-b) =2S/(a+c-b)
r_b1= 12√5/4 =3√5
r_b2= 12√5/2 =6√5