Пошаговое объяснение:
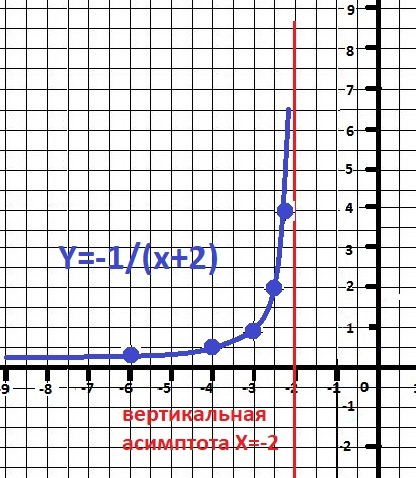
1. ДАНО: Y = - 1/(x+2), X∈(-∞;-2) или D(y) = {-∞;-2}
x+2 ≠0, X≠ -2 - разрыв не входит в область определения. Вертикальная асимптота - Х = -2.
Получаем одну ветвь графика - Y = - 1/(x+2), Поведение на бесконечности: Y(-∞) = 0, limY(x->-2) = +∞. Вычисляем, например при Х = - 2,5 и получаем Y(-2.5) = 2
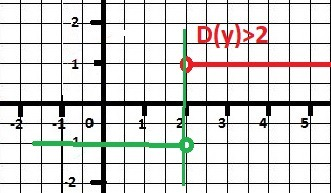
3. Разрыв при Х=2 - могла бы быть вертикальная асимптота, но область определения - правая часть графика - красная.
График на рисунке в приложении.
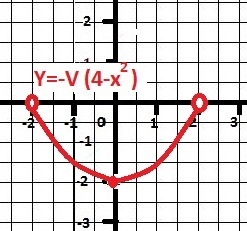
2. ДАНО: Y = - √(4 - x²), D(y) ={-2;2}.
Под корнем - неотрицательное число, как раз в области определения. Значения х = +/-2 - исключаем - "дырки". Сам корень - положительный, на графике становится отрицательным.
Под корнем - х ² - на графике - два фрагмента графика корня.
3.