Ответ:
58 ед. пл.
Пошаговое объяснение:
Черный единичный кубик мистера Фокса имеет 6 черных граней единичной площади.
Если Мистер Фокс строит параллелепипед, стараясь, чтобы он был красивым при наибольшей площади черной области, то он должен:
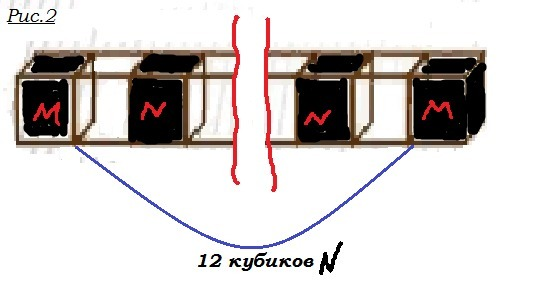
1. разместить черные кубики в вершинах параллелепипеда. Там их черные грани будут располагаться в трех гранях построенного параллелепипеда, т.е. видны будут три грани из шести . Т.е. в каждой вершине параллелепипеда, а их 8, будет черный кубик, с видимой площадью черной области 3 ед. пл. Это кубики а на рис. 1.
3*8 = 24 ед.пл. ---- площадь черной области в вершинах параллелепипеда.
2. 14 - 8 = 6 кубиков, которым не хватило места в вершинах. Их мистер Фокс должен располагать на ребрах, так, чтобы две единичные черные грани располагались на двух соседних гранях параллелепипеда. Всего ребер в параллелепипеде 12, надо только, чтобы их длина была больше двух единичных отрезков, чтобы можно было разместить кубики между вершинами. Это кубики б, показывающие черные участки 2 ед. пл
2 * 6 = 12 ед.пл. ---- площадь черных областей на ребрах кубиков б
24 + 12 = 36 ед. пл ---- максимально возможная площадь черной области при таком построении
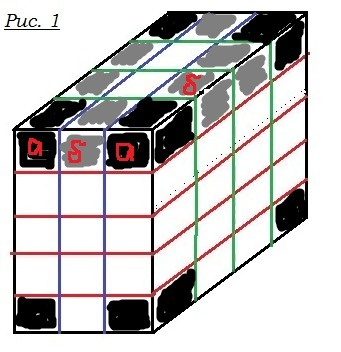
Но, если мистер Фокс задался целью построить параллелепипед с максимально возможной общей площадью, он, желая, чтобы черный кубик показывал максимальное число черных граней, составит их в один ряд, (рис. 2) Два крайних 1-ый и 14-ый (тип M) покажут 5 граней из 6, т.е.
5 * 2 = 10 ед.пл. ----- их общая площадь
14 - 2 = 12 --- число кубиков в середине (тип N)
Кубики в середине, с 2-го по 13-ый, покажут только 4 грани.
4 * 12 = 48 ед.пл. ------ суммарная площадь видимой поверхности черных кубиков в середине.
10 + 48 = 58 ед. пл. ---- суммарная возможная площадь.
Мистер Фокс может располагать в ряду между черными кубиками любое число белых, но на суммарную площадь черной области это влиять не будет.