Дано:
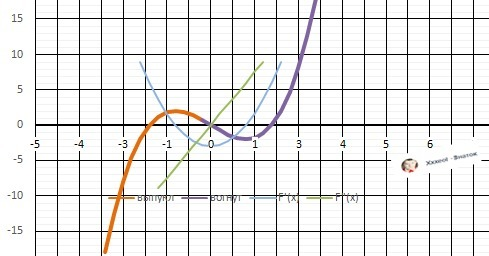
f(x) = x³ - 3*x
Пошаговое объяснение:
1) Находим экстремумы функции по первой производной.
f'(x) = 3*x² - 3 = 3*(x²-1) = 3*(x-1)*(x+1) = 0.
Экстремумы в точках Х1 = -1 и Х2 = 1.
Убывает между корней - Х=[-1;1]
Возрастает - X = (-∞;-1]∪[1;+∞)
Рисунок с графиком в приложении.